Tajanstvene crvotočine: Matematički modeli koji otkrivaju putovanja kroz prostor-vreme

Dobro došli u fascinantan svet teorijske fizike, gde se matematički modeli pretvaraju u mostove između udaljenih delova svemira! Crvotočine, ili wormholes na engleskom, predstavljaju hipotetske „tunele“ u prostor-vremenu koji bi mogli omogućiti brza putovanja kroz ogromne kosmičke udaljenosti, ili čak putovanje kroz vreme. Ovi koncepti nisu samo stvar naučne fantastike – oni su duboko ukorenjeni u opštoj teoriji relativnosti Alberta Einsteina. U ovom članku, namenjenom naučnom blogu, detaljno ćemo istražiti ključne matematičke modele crvotočina. Dodali smo još više pojašnjenja za lakše razumevanje, uključujući korak-po-korak objašnjenja jednadžbi, njihove implikacije i kako se oni povezuju sa stvarnim fizičkim problemima. Takođe, obogatili smo tekst dijagramima i ilustracijama da bismo vizuelno prikazali ove apstraktne ideje, čineći ih pristupačnijim za širu publiku.

Počnimo od osnova: Einsteinove poljske jednačine su srce svih ovih modela. One opisuju kako masa i energija savijaju prostor-vreme: Rμν−12Rgμν=8πGc4TμνR_{\mu\nu} – \frac{1}{2} R g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu}Rμν​−21​Rgμν​=c48πG​Tμν​. Leva strana predstavlja geometriju prostor-vremena (zakrivljenost), dok desna strana predstavlja izvore te zakrivljenosti (masa, energija). Da bismo stvorili model crvotočine, fizičari pretpostavljaju određene simetrije (kao što je sferična simetrija) i umeću metriku – matematički opis prostor-vremena – u ove jednadžbe. Zatim rešavaju za oblik funkcije i potrebnu „materiju“ koja bi održala tunel otvorenim. Ovo nije lako; često zahteva egzotičnu materiju sa negativnom energijskom gustinom, što još uvek nije otkriveno u prirodi, ali se istražuje kroz kvantnu fiziku.

1. Schwarzschildova Crvotočina (Einstein-Rosen Most)

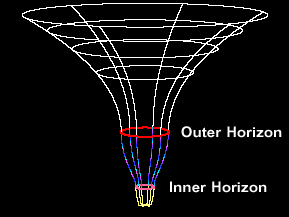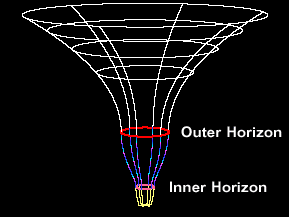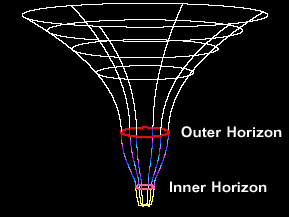
Ovo je najstariji model, predložen 1935. godine od strane Alberta Einsteina i Nathana Rosena. On predstavlja most između dve regije svemira, ali nije prolazan – to jest, ne možete kroz njega proći pre nego što se uruši. Zamislite ga kao privremeni tunel koji povezuje dve crne rupe: jednu „crnu“ (koja usisava materiju) i jednu „belu“ (koja je izbacuje).

• Metrika (matematički opis): U sferičnim koordinatama, ovo je Schwarzschildova metrika za crnu rupu: ds2=−c2(1−2GMrc2)dt2+dr21−2GMrc2+r2(dθ2+sin⁡2θ dϕ2)ds^2 = -c^2 \left(1 – \frac{2GM}{rc^2}\right) dt^2 + \frac{dr^2}{1 – \frac{2GM}{rc^2}} + r^2 (d\theta^2 + \sin^2\theta \, d\phi^2)ds2=−c2(1−rc22GM​)dt2+1−rc22GM​dr2​+r2(dθ2+sin2θdϕ2) Ovde, rs=2GM/c2r_s = 2GM/c^2rs​=2GM/c2 je Schwarzschildov radijus, granica iza koje ništa ne može pobegnuti. Ova jednadžba pokazuje kako se vreme usporava blizu masivnog objekta i kako se prostor savija.
• Kako doći do modela (korak-po-korak): Počnite sa vakuumskim rešenjem (gde nema materije, Tμν=0T_{\mu\nu} = 0Tμν​=0). Koristite Kruskal-Szekeres koordinate da proširite prostor-vreme iza horizonta događaja. Zatim zamenite $r$ sa u2=r−2mu^2 = r – 2mu2=r−2m (u geometrijskim jedinicama gde $G=c=1$, i m=GM/c2m = GM/c^2m=GM/c2): ds2=−4(u2+2m) du2−(u2+2m)2(dθ2+sin⁡2θ dϕ2)+u2u2+2m dt2ds^2 = -4(u^2 + 2m) \, du^2 – (u^2 + 2m)^2 (d\theta^2 + \sin^2\theta \, d\phi^2) + \frac{u^2}{u^2 + 2m} \, dt^2ds2=−4(u2+2m)du2−(u2+2m)2(dθ2+sin2θdϕ2)+u2+2mu2​dt2 Most se nalazi na $u=0$, povezujući dve „ploče“ svemira. Ovo pokazuje da crvotočina nije stabilna; urušava se zbog singularnosti (tačke beskonačne gustine).
• Problemi i implikacije: Ovaj model objašnjava zašto crvotočine nisu lako prolazne – zahtevaju belu rupu, koja možda ne postoji u našem svemiru. U naučnoj fantastici, poput filma „Interstellar“, ovo se koristi za putovanja, ali u stvarnosti, prolaz bi bio nemoguć zbog ekstremnih sila. Evo dijagrama koji vizuelno prikazuje ovaj most:

dcc.ligo.org

The Einstein-Rosen Bridge and the Schwarzschild Wormhole

2. Morris-Thorne Crvotočina

Ovaj model, predložen 1988. godine od Michaela Morrisa i Kipa Thornea, je prvi prolazan – omogućava putovanje kroz tunel bez urušavanja. Ključ je egzotična materija koja drži „grlo“ (najužu tačku) otvorenim, poput nevidljive „podupiračke strukture“.

• Metrika: Statična i sferična, što znači da se ne menja vremenom i simetrična je oko tačke:

  ds2=−e2Φ(r)dt2+dr21−b(r)r+r2(dθ2+sin⁡2θ dϕ2)ds^2 = -e^{2\Phi(r)} dt^2 + \frac{dr^2}{1 – \frac{b(r)}{r}} + r^2 (d\theta^2 + \sin^2\theta \, d\phi^2)ds2=−e2Φ(r)dt2+1−rb(r)​dr2​+r2(dθ2+sin2θdϕ2)

  Funkcija $\Phi (r)$ kontroliše pomeranje vremena (redshift), a $b(r)$ oblik tunela. Grlo je na r0r_0r0​ gde b(r0)=r0b(r_0) = r_0b(r0​)=r0​, i za prolaznost mora važiti b′(r0)<1b'(r_0) < 1b′(r0​)<1 (uslov „flare-out“ – tunel se širi posle grla) i $\Phi (r)$ mora biti konačna (bez horizonta događaja).

• Kako doći do modela (korak-po-korak): Umesto da počnete od materije, obrnuto: pretpostavite metriku i izračunajte potrebni tenzor energije-momenta TμνT_{\mu\nu}Tμν​ iz Einsteinovih jednadžbi. Koristeći ortonormalni okvir (kao što su lokalne koordinate putnika), komponenti su:

  • Gustoća energije: ρ(r)=b′(r)8πr2\rho(r) = \frac{b'(r)}{8\pi r^2}ρ(r)=8πr2b′(r)​ (mora biti negativna za stabilnost).
  • Radijalni pritisak: pr(r)=−b(r)8πr3+2r−b(r)8πr2Φ′(r)p_r(r) = -\frac{b(r)}{8\pi r^3} + 2\frac{r- b(r)}{8\pi r^2} \Phi'(r)pr​(r)=−8πr3b(r)​+28πr2r−b(r)​Φ′(r).
  • Transverzalni pritisak: pt(r)=(r−b(r))[Φ′′(r)+(Φ′(r))2+Φ′(r)r−b′(r)r−b(r)2r2(1−b(r)/r)Φ′(r)]/8πp_t(r) = (r – b(r)) \left[ \Phi“(r) + (\Phi'(r))^2 + \frac{\Phi'(r)}{r} – \frac{b'(r)r – b(r)}{2r^2 (1 – b(r)/r)} \Phi'(r) \right] / 8\pipt​(r)=(r−b(r))[Φ′′(r)+(Φ′(r))2+rΦ′(r)​−2r2(1−b(r)/r)b′(r)r−b(r)​Φ′(r)]/8π.

  Ovo krši nultu energijsku uslov (NEC: $\rho +p\ge 0$), jer je ρ+pr<0\rho + p_r < 0ρ+pr​<0 na grlu – zahteva egzotičnu materiju koja odbija gravitaciju. U stvarnosti, ovo bi moglo biti povezano sa kvantnim efektima poput Casimirovog efekta.

• Ugrađivanje (embedding) za vizualizaciju: Da bismo „videli“ tunel u 3D prostoru, koristimo jednadžbu: dzdr=±r/b(r)−11−b(r)/r\frac{dz}{dr} = \pm \sqrt{\frac{r/b(r) – 1}{1 – b(r)/r}}drdz​=±1−b(r)/rr/b(r)−1​​. Ovo stvara sliku tunela koji se širi sa obe strane grla, poput levka spojena sa drugim levkom.

researchgate.net

Embedding diagram of the Morris-Thorne wormhole metric with …

Evo još jednog embedding dijagrama za prolaznu crvotočinu, koji pokazuje kako se dve udaljene regije povezuju:

researchgate.net

Embedding Diagram For A Traversable Wormhole That Connects Two …

3. Ellisova Crvotočina (Varijanta Morris-Thorne)

Ova je slična prethodnoj, ali sa specifičnim funkcijama i bez gravitacije (nulta masa). Metrika:

ds2=−c2dt2+dℓ2+(k2+ℓ2)(dθ2+sin⁡2θ dϕ2)ds^2 = -c^2 dt^2 + d\ell^2 + (k^2 + \ell^2) (d\theta^2 + \sin^2\theta \, d\phi^2)ds2=−c2dt2+dℓ2+(k2+ℓ2)(dθ2+sin2θdϕ2)

Ovde, $\ell$ je pravilna radijalna udaljenost, a $k$ parametar koji određuje širinu grla. Ovo je specijalan slučaj gde crvotočina ne privlači materiju, čineći je idealnom za teoretske simulacije.

• Kako doći do modela: Počnite sa „drainhole“ modelom Harolda G. Ellisa, gde parametar $m$ predstavlja gravitacionu snagu, a $n$ zakrivljenost. Postavite $m=0$ za nongravitirajući tunel. Ovo pokazuje da čak i bez mase, egzotična materija je neophodna za stabilnost.

4. Nabijene Crvotočine (Reissner-Nordström)

Ovo je proširenje Schwarzschildovog modela sa električnim nabojem, što dodaje elektromagnetizam u mešavinu.

• Metrika: ds2=−(1−2mr+ε2r2)dt2+dr21−2mr+ε2r2+r2(dθ2+sin⁡2θ dϕ2)ds^2 = -\left(1 – \frac{2m}{r} + \frac{\varepsilon^2}{r^2}\right) dt^2 + \frac{dr^2}{1 – \frac{2m}{r} + \frac{\varepsilon^2}{r^2}} + r^2 (d\theta^2 + \sin^2\theta \, d\phi^2)ds2=−(1−r2m​+r2ε2​)dt2+1−r2m​+r2ε2​dr2​+r2(dθ2+sin2θdϕ2) Sa nabojem $\epsilon$. Zamena u2=r2−ε2/2u^2 = r^2 – \varepsilon^2/2u2=r2−ε2/2 daje bezsingularnu formu, što znači da nema tačke beskonačne gustine.
• Kako doći do modela: Dodajte Maxwellov tenzor (za elektromagnetizam) u TμνT_{\mu\nu}Tμν​ i rešite za nabijenu crnu rupu. Naboj odbija materiju, čineći tunel potencijalno stabilnijim.

jila.colorado.edu

Charged Black Holes: The Reissner-Nordström Geometry

5. Noviji Modeli u Modificiranim Gravitacijama

U savremenim teorijama, poput F(Q, L_m, T) gravitacije (simetrična teleparalelna gravitacija), crvotočine se mogu formirati sa manje egzotične materije. Metrika je slična Morris-Thorne, ali sa non-metričnim skalarom Q.

• Kako doći do modela: Varijajte akciju S=116π∫F(Q,Lm,T)−g d4x+∫Lm−g d4xS = \frac{1}{16\pi} \int F(Q, L_m, T) \sqrt{-g} \, d^4x + \int L_m \sqrt{-g} \, d^4xS=16π1​∫F(Q,Lm​,T)−g​d4x+∫Lm​−g​d4x, i rešite za anizotropnu tečnost. Funkcija oblika: b(r)=P−Pr5/[Pr4+rt4(rt−P)e2μ(1/rt−1/r)]+rb(r) = P – P r^5 / [P r^4 + r_t^4 (r_t – P) e^{2\mu (1/r_t – 1/r)}] + rb(r)=P−Pr5/[Pr4+rt4​(rt​−P)e2μ(1/rt​−1/r)]+r, sa $\Phi (r)=-2\mu /r$. Ovo krši energijske uslove samo blizu grla, čineći ih realnijim.

Takođe, u višim dimenzijama (npr. 6D), koriste se proširene Einsteinove jednadžbe sa kozmološkom konstantom, što omogućava složenije tunele.

profmattstrassler.com

Wormholes in a Lab? How About String Theory & Extra Dimensions Too?

U zaključku, ovi modeli su teoretski dragulji koji nam pomažu da razumemo granice fizike, ali ostaju daleko od praktične realizacije zbog egzotične materije i energetskih zahteva. Oni inspirišu istraživanja u kvantnoj gravitaciji i možda jednog dana otvore vrata međuzvezdanim putovanjima. Ako želite simulacije ili dodatne jednadžbe, javite se u komentarima!