Dobro došli nazad u svet teorijske fizike, gde istražujemo granice mogućeg! Pitanje o „uvrtanju“ potencijalne crvotočine (wormhole) tako da putanja postane poput „fišeka“ (mislimo na spiralnu ili cilindričnu putanju sa uvrtanjem, slično stabilizaciji municije kroz rotaciju) je fascinantno i duboko hipotetičko. U opštoj teoriji relativnosti, crvotočine su tuneli koji povezuju udaljene tačke u prostor-vremenu, ali dodavanje rotacije (uvrtanja) i sabijanja (kompresije) uvodi složene efekte poput uvlačenja prostor-vremena (frame-dragging) i promena u zakrivljenosti. Ovo nije samo mašta – postoje matematički modeli rotirajućih crvotočina koji opisuju šta bi se moglo dogoditi.
U ovom članku, detaljno ćemo istražiti ove efekte, sa korak-po-korak pojašnjenjima, matematičkim osnovama i vizuelnim ilustracijama. Počnimo od osnova: rotacija u relativnosti nije samo okretanje objekta – ona savija i „uvrće“ samo prostor-vreme oko sebe, što može uticati na putanje svetlosti, materije i čak vremena. Ako bismo „uvrnuli“ crvotočinu, putanja kroz nju bi postala spiralna, a prostor u sredini (u „toku fišeka“) bi doživeo ekstremne deformacije, uključujući jače plimne sile i moguće generisanje magnetnih polja. Međutim, ovo zahteva egzotičnu materiju da održi stabilnost, i još uvek je čisto teoretsko, bez eksperimentalnih dokaza.
Osnovni efekti uvrtanja crvotočine
Kada dodamo rotaciju crvotočini, ona postaje slična rotirajućoj crnoj rupi (kao u Kerr metriki), ali sa prolaznim tunelom umesto singularnosti. Rotacija izaziva frame-dragging efekt (Lense-Thirring efekt), gde se prostor-vreme „uvlači“ sa rotacijom, poput meda koji se meša. Ako putanja postane „fišekasta“ (spiralna sa sabijanjem), to bi značilo da se tunel savija u spiralu, sa kompresijom duž ose.
- Šta se dešava sa prostorom u sredini? U sredini (u „toku fišeka“), zakrivljenost postaje nejednaka – jača na ekvatoru (ekvatorskoj ravni rotacije), što koncentriše plimne sile. Ovo može dovesti do „kidanje“ putanja čestica, gde se one spiralno uvlače, slično vrtlogu. Sabijanje (kompresija) bi povećalo gustinu energije, možda kršeći energijske uslove, ali rotacija može stabilizovati tunel, omogućavajući putovanje bez urušavanja. Međutim, pregrevanje ili vremenski paradoksi (poput putovanja u prošlost) bi bili rizici.
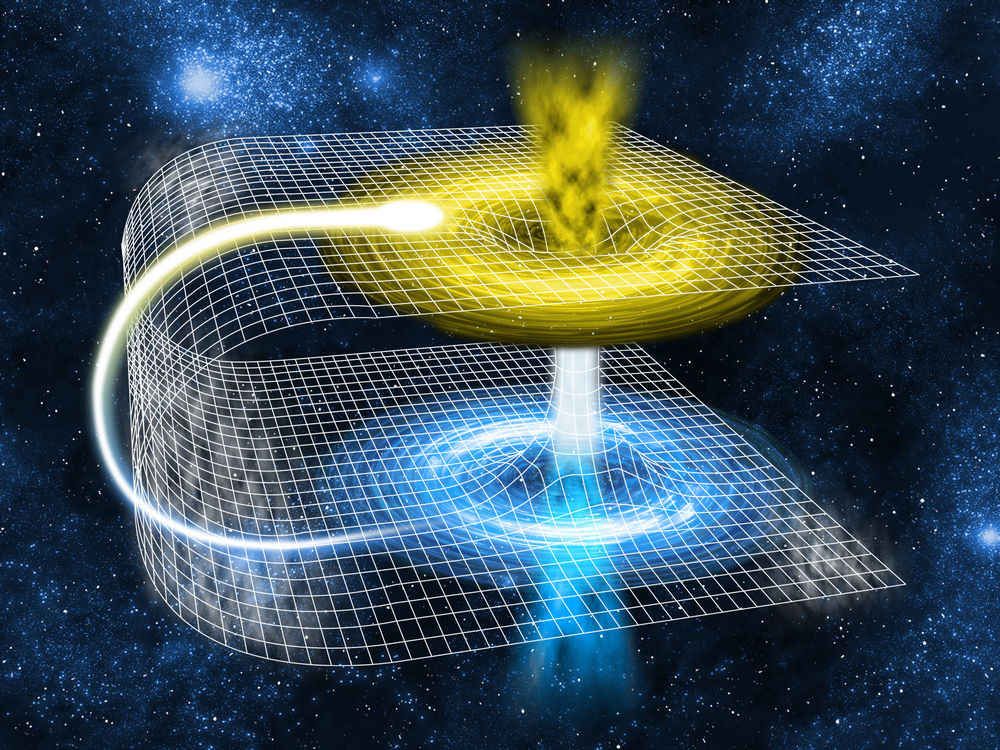
Evo ilustracije kako bi izgledala rotirajuća crvotočina, sa uvrtanjem prostor-vremena:
Matematički modeli rotirajućih crvotočina
Modeli se temelje na proširenjima standardnih crvotočina (poput Morris-Thorne) sa rotacijom. Počinjemo od Einsteinovih poljskih jednačina, ali dodajemo ugaoni moment (spin). Korak-po-korak, evo ključnih modela i efekata.
1. Kerr-Like Wormholes (Rotirajući Kerr modeli)
Ovo je proširenje Kerr metrike za rotirajuće crne rupe na crvotočine. Ako „uvrnemo“ crvotočinu, ona dobija ugaoni moment, čineći putanju spiralnom.
- Metrika (osnovni opis): Kerr metrika u Boyer-Lindquist koordinatama: ds2=−(1−2Mrρ2)dt2−4Marsin2θρ2dtdϕ+ρ2Δdr2+ρ2dθ2+Σsin2θρ2dϕ2ds^2 = -\left(1 – \frac{2Mr}{\rho^2}\right) dt^2 – \frac{4Mar \sin^2\theta}{\rho^2} dt d\phi + \frac{\rho^2}{\Delta} dr^2 + \rho^2 d\theta^2 + \frac{\Sigma \sin^2\theta}{\rho^2} d\phi^2 Gde je ρ2=r2+a2cos2θ\rho^2 = r^2 + a^2 \cos^2\theta, Δ=r2−2Mr+a2\Delta = r^2 – 2Mr + a^2, Σ=(r2+a2)2−a2Δsin2θ\Sigma = (r^2 + a^2)^2 – a^2 \Delta \sin^2\theta, a je parametar rotacije (a = J/M, J ugaoni moment).
- Kako doći do modela (korak-po-korak): Počnite sa statičkom crvotočinom (kao Schwarzschild). Dodajte rotaciju koristeći Ehlers transformacije (matematički alat za generisanje rotirajućih rešenja). Zatim, modifikujte da izbegnete singularnost: Zamijenite crnu rupu tunelom, koristeći egzotičnu materiju da održite grlo otvorenim. Rotacija dodaje off-diagonalni termin (dt dφ), koji predstavlja frame-dragging – prostor se „uvrće“ sa rotacijom.
- Efekti na prostor u sredini: U sredini tunela, rotacija koncentriše zakrivljenost na ekvatoru, uzrokujući jače plimne sile (tidal forces). Sabijanje bi povećalo efekat, možda stvarajući „vrtlog“ gde se vreme usporava ili ubrzava zavisno od smera putovanja. Ovo može generisati magnetna polja ako su prisutne nabijene čestice. Evo embedding dijagrama za Kerr-like crvotočinu, pokazujući spiralno uvrtanje:arxiv.org
2. Rotating Wormholes u Einstein-Dirac-Maxwell teoriji
Ovi modeli uključuju spinorne polja (fermione) i elektromagnetizam za podršku rotaciji.
- Metrika: Slična Kerr, ali sa dodatnim terminima za spinor polje. Primer: ds2=−N2dt2+grrdr2+gθθdθ2+gϕϕ(dϕ−ωdt)2ds^2 = -N^2 dt^2 + g_{rr} dr^2 + g_{\theta\theta} d\theta^2 + g_{\phi\phi} (d\phi – \omega dt)^2 Gde ω je ugaona brzina, a N je lapse funkcija.
- Kako doći do modela: Rešite Einsteinove jednačine sa Diracovim jednačinama za spinore (koji pružaju negativnu energiju). Dodajte Maxwellov tenzor za električna polja. Rotacija se uvodi preko ugaonog momenta spinora, čineći tunel stabilnijim.
- Efekti na prostor u sredini: U „toku fišeka“, sabijanje i uvrtanje bi doveli do nejednake zakrivljenosti – prostor bi se „stisnuo“ axialno, ali širio ekvatorski, uzrokujući spiralne putanje. Ovo može omogućiti putovanje kroz vreme (CTC – closed timelike curves), ali sa rizikom od paradoksa. Ilustracija pokazuje talase u prostor-vremenu izazvane rotacijom:arxiv.org
3. Rotating Wormholes sa Tri-Form poljima
Noviji modeli koriste tri-form polja (višedimenzionalna polja) za podršku rotaciji bez mnogo egzotične materije.
- Metrika: Proširena Morris-Thorne sa rotacijom: ds2=−e2Φdt2+e2Λdr2+r2(dθ2+sin2θ(dϕ−Ωdt)2)ds^2 = -e^{2\Phi} dt^2 + e^{2\Lambda} dr^2 + r^2 (d\theta^2 + \sin^2\theta (d\phi – \Omega dt)^2) Ω je funkcija rotacije.
- Kako doći do modela: Integrirajte tri-form tenzor u T_{\mu\nu}, rešavajući za parametre koji omogućavaju stabilnost. Rotacija se dodaje preko Ω, koji zavisi od r.
- Efekti na prostor u sredini: Sabijanje bi povećalo gustinu polja, čineći sredinu „vrtložnom“ – prostor bi se uvijao, uzrokujući efekte poput gravitacionih talasa ili magnetnih polja iz pokreta nabijenih čestica. Evo dijagrama rotirajućeg tunela:sciencedirect.com
Rizici i mogućnosti
U hipotetičkom scenariju sa uvrtanjem i sabijanjem, crvotočina bi postala dinamički vrtlog, gde prostor u sredini doživljava ekstremne deformacije – jače plimne sile, spiralne putanje i moguće putovanje kroz vreme. Međutim, ovo bi zahtevalo ogromnu energiju i egzotičnu materiju, sa rizicima od urušavanja ili paradoksa. Ovi modeli inspirišu istraživanja, ali su daleko od realnosti.